EdDSA. Исследуем криптоподпись и учимся с ней бороться

В сегодняшней статье я хочу помучить тебя самым ненавистным для некоторых студентов предметом — высшей математикой. А именно рассказать о распространенном, но малоизвестном алгоритме криптоподписи EdDSA + SHA-512.

warning

Статья имеет ознакомительный характер и предназначена для исследователей безопасности и специалистов по разработке защиты программного обеспечения. Автор и редакция не несут ответственности за любой вред, причиненный с применением изложенной информации. Нарушение авторских прав и патентного законодательства, распространение контрафактного ПО и нарушение работы систем преследуются по закону.

Каждый уважающий себя хакер просто обязан знать врага в лицо и разбираться в основных криптоалгоритмах, популярных и не очень. Так, криптоподпись EdDSA, несмотря на довольно широкое использование (I2P, OpenBSD, OpenSSH и так далее), в отличие от своей эллиптической сестры EcDSA сильно обделена реализациями в стандартных криптобиблиотеках. Ее можно найти разве что в узкоспецифических проектах типа NaCl, SUPERCOP, python-ed25519 и прочей экзотике.

Сложностей добавляет и то, что по упомянутой причине каждый автор реализует хеширование, а также генерацию ключей и сигнатур по‑своему. Поэтому я и решил поподробнее рассказать об алгоритме EdDSA, причем именно с практической точки зрения. Мы разберем реализацию и работу этой подписи на конкретном примере.

Предмет исследования

Предметом нашего исследования станет некое приложение, при первом запуске скачивающее триальную лицензию с сервера. После несложных телодвижений в ProcMon скачанная лицензия благополучно обнаруживается в реестре.

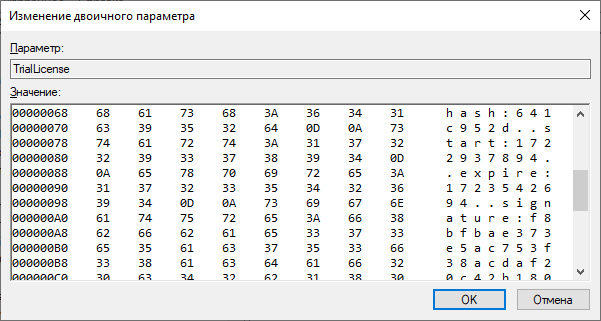
Кажется, что все в ней прекрасно: в понятном текстовом виде хранится и версия, и ID оборудования, а также время начала и конца срока действия в миллисекундах. Можно смело править и пользоваться! Но нет, в конце мы обнаруживаем поле с недвусмысленным именем signature, где в шестнадцатеричном виде закодирован некий 64-байтовый (512-битный) блок данных.

F8 BF BA E3 73 E5 AC 75 3F 38 AC DA F2 0C 42 B1 80 0C 18 A0 BF 92 8F 39 5C B1 A1 8E 2E E7 47 62
F1 3A E7 94 2A 5F 61 6D 97 5F 76 5B FD 82 B6 58 A0 D7 4C 07 3B 7E 61 A1 B3 85 75 62 93 94 90 06

Действительно ли это сигнатура или подпись текстовых данных лицензии, проверить элементарно: замена любого байта в текстовой части или в самой сигнатуре делает лицензию невалидной, и программа немедленно кидается повторно скачивать ее с удаленного сервера. Первый 512-битный хеш, который приходит в голову, — это SHA-512, его наличие подтверждает и программа Krypto Analyzer, если скормить ей наш исполняемый модуль.

То, что это не случайный набор байтов, а реальная инициализация подсчета хеша SHA-512, нам подтверждает и IDA, в которой мы открываем код приложения по любезно предоставленному нам анализатором адресу.

Однако счастье оказывается не так близко, как кажется: посчитанная контрольная сумма SHA-512 совершенно не похожа на значение signature, а значит, для подписи не годится. Подпись считается каким‑то иным способом.

Попробуем копнуть с другой стороны: найти проверку подписи в отладчике. Загружаем нашу программу в x64dbg и ищем проверку подписи. Программа написана на чистом C++, ничем не защищена и свободна от антиотладчиков, поэтому искомое место находится элементарно, в псевдокоде IDA оно выглядит так.

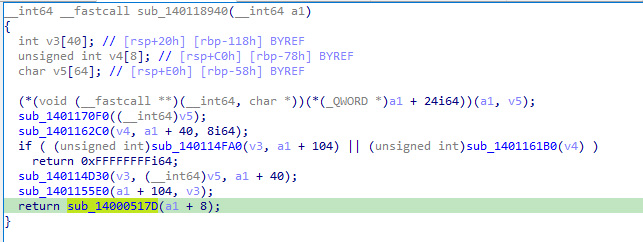
Будь мы чуть более ленивыми, то закоротили бы эту функцию на return 0 (да, при успешной верификации она возвращает именно 0) и успокоились бы, но тогда смысла писать эту статью не было бы никакого. Попробуем все‑таки разобраться, как устроена сигнатура и как она верифицируется.

Очевидно, что финальную проверку выполняет функция sub_14000517D, которая сложным и непрямым способом сравнивает на тождественное равенство две 32-байтовые последовательности. Первую из них IDA-шный декомпилятор условно обзывает a1 + 8. Она представляет собой первые 32 байта сигнатуры, то есть в нашем случае выглядит так:

F8 BF BA E3 73 E5 AC 75 3F 38 AC DA F2 0C 42 B1 80 0C 18 A0 BF 92 8F 39 5C B1 A1 8E 2E E7 47 62

Вторая последовательность вычисляется функцией sub_1401155E0 и условно называется a1 + 104. Оставим пока без внимания тревожный звоночек «почему проверяется только первая половина сигнатуры, зачем тогда вторая?» и тупо попробуем переподписать лицензию значением a1 + 104. То есть меняем в текстовой части лицензии любой байт, ставим точку останова на проверку, берем новое значение a1 + 104 и подставляем его вместо первых 32 байт сигнатуры.

План кажется надежным, как швейцарские часы, но он не работает: после замены первой половины сигнатуры значение a1 + 104 снова меняется. Это означает, что первая половина сигнатуры входит в обе части этого криптоуравнения. Вторая половина сигнатуры тоже находится довольно быстро — она под условным именем a1 + 40 является аргументом функций sub_1401162C0 и sub_140114D30 в цепочке весьма головоломного расчета проверочного значения a1 + 104.

Попробуем все‑таки опознать криптоалгоритм. Потыкавшись по функциям, ничего характерного не обнаруживаем, лишь какие‑то долгие, ломающие мозг вычисления, напоминающие операции с BigInteger, коими они, очевидно, и являются. Самой перспективной в этом плане представляется функция sub_1401161B0.

Помимо того что она визуально красива и интуитивно понятна, эта функция содержит массу волшебных цифр. Собственно, ее смысл заключается в том, что она возвращает старшие 32 бита суммы второй половины сигнатуры a1 + 40 и некоего магического 256-битного числа:

EFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEB2106215D086329A7ED9CE5A30A2C13

Причем, если результат будет ненулевой, сигнатура признается негодной. Само число нам ни о чем не говорит и нигде в интернете не упоминается, однако если предположить, что проверяется именно не превышение значения, обратного этому числу, а именно
1000000000000000000000000000000014def9dea2f79cd65812631a5cf5d3ed, то пазл начинает складываться.

1000000000000000000000000000000014def9dea2f79cd65812631a5cf5d3ed

Если перевести младшую часть этого значения в десятичный вид, мы получим

27742317777372353535851937790883648493

А это довольно известная константа! Причем известная именно в таком сочетании — в виде суммы с двойкой в 252-й степени (2^252 + эта константа). Это так называемый порядок (order) базовой точки кривой Эдвардса, использующейся криптоалгоритмом EdDSA.

Вот мы и подошли к главной цели нашего повествования. Как и обещал с самого начала, я не буду сильно загружать тебя математической теорией эллиптической криптографии и особенностями реализации этих самых кривых Эдвардса.

www

Желающие могут самостоятельно вкатиться в эту увлекательную тему на Вики, чуть менее подробно, но более доходчиво тема описана на xmr.ru и в цикле статей на Хабре.

Наконец, для совсем продвинутых отличников доступна англоязычная литература по использованию кривых Эдвардса в криптографии.

Для всех тех, кому читать всю эту теорию лень и неинтересно, попробую объяснить суть задачи на пальцах, чтобы хотя бы базовые принципы дальнейшего обсуждения стали ясны.

Начну с самого главного и весьма прискорбного факта: эллиптическая криптография асимметрична. Те, кто уже сталкивались, например, с RSA, знают, что это такое: для каждой подписи есть два ключа. Один (закрытый, секретный) — у разработчика, с помощью этого ключа он и формирует подпись. И открытый (публичный) — у пользователя, который проверяет этим ключом валидность подписи. Сделано это для того, чтобы ты никак не смог подделать подпись на измененной лицензии. Как это ни грустно звучит, в нашем примере мы тоже не сможем этого сделать при всем желании.

Однако мы можем создать собственную подпись, сгенерировав пару ключей и подменив публичный ключ в приложении своим. Не буду объяснять, чем патч публичного ключа лучше гораздо более простого патча верификации сигнатуры, ведь наше исследование преследует не вредоносную, а чисто познавательную цель.

Итак, попробуем разобраться в алгоритме проверки подписи, сгенерировать свою пару ключей, найти в нашем приложении публичный ключ и, поменяв его, переподписать лицензию новой подписью.

Теория

Обратиться к теории нам все‑таки придется. Для начала определимся, что же такое эллиптическая кривая. Тем, кто не прочитал научные определения по приведенным выше ссылкам или прочитал, но ничего не понял, даю полезный совет: забудь как минимум картинки, которые ты там видел. На самом деле это никакая не эллиптическая и никакая не кривая.

На практике это чудовищно огромное, но конечное дискретное множество точек, причем множество упорядоченное. Каждая точка имеет два целочисленных параметра — координаты X и Y, фактически псевдослучайные, вычисляемые по очень сложным формулам. Ты спросишь: каким образом множество упорядочено?

На нем определили операции сложения точки со скалярной константой и другой (или той же самой) точкой. Причем через операцию сложения с самой собой определена и операция умножения. На этом множестве также определена базовая точка (которую называют B или, как больше любят женщины, точка G). Поскольку рассматриваемое нами множество, называемое эллиптической кривой, замкнуто и ограниченно, то через определенное число шагов складывания с самой собой точка G переходит в себя же. То есть G = G * L.

Вот это самое волшебное число L и называется порядком базовой точки кривой Эдвардса, проверку на превышение которого мы нашли в функции sub_1401161B0. Все вычисления в алгоритме делаются по модулю L, соответственно, скалярная константа, превышающая L, заведомо ошибочна, именно поэтому и выполняется проверка.

Попробую теперь наглядно описать процесс подписи лицензии и ее проверки при помощи алгоритма EdDSA. Для простоты и удобства забудем пока про реальные координаты X и Y каждой точки и нарисуем множество E в виде замкнутой эллиптической кривой. Изобразим базовую точку G на ней. В этом случае операции сложения и умножения точки на кривой будут представимы просто в виде перемещения точки по кривой на определенное число шагов.

Выберем в качестве закрытого ключа любое случайное число, меньшее порядка кривой s < L, тогда открытым (публичным) ключом будет точка A на кривой, равная A = G * s. Суть несимметричной криптографии заключается в том, что скорость обратной к умножению операции просто несоизмеримо ниже, чем само умножение. То есть получить приватный ключ из секретного в нашей реализации (32-байтовые или 256-битные операнды) можно мгновенно, а обратная задача на актуальном железе может считаться целую вечность.

Выберем теперь некое произвольное число r < L (на самом деле не совсем произвольное: в разных реализациях его для пущей жести ставят в зависимость от секретного ключа и даже от хеша подписываемого сообщения). Теперь создадим соответствующую ему точку R = r * G. Далее считаем хеш от подписываемых данных (назовем его просто HASH). Считать его можно как угодно, хеш‑функция может быть произвольной, количество битов хеша должно составлять 512, хотя потом это значение все равно нормируется по модулю L.

Именно поэтому определенное распространение получила связка EdDSA + SHA-512, которую мы сейчас и разбираем. Несмотря на произвольность реализации, по канону положено, чтобы в хешируемые данные обязательно входил открытый ключ (двоичное представление точки A) и двоичное представление точки R. Для чего это сделано, ты, надеюсь, уже понял, попробовав поменять значение R в сигнатуре (а это и есть первые 32 байта сигнатуры). Второй половиной сигнатуры будет число S = r + HASH * s. В общем, процесс подписи выглядит примерно так, как показано на рисунке, сигнатура выделена зеленым.

Попробуем теперь верифицировать полученную подпись. Берем значение S (вторые 32 байта сигнатуры) и умножаем на базовую точку G. Получаем новую точку G * S, затем считаем значение HASH вышеописанным образом, умножаем его на публичный ключ A и получаем еще одну точку A * HASH. А затем просто считаем разность между ними. Если верификация проходит, должна получиться точка R.

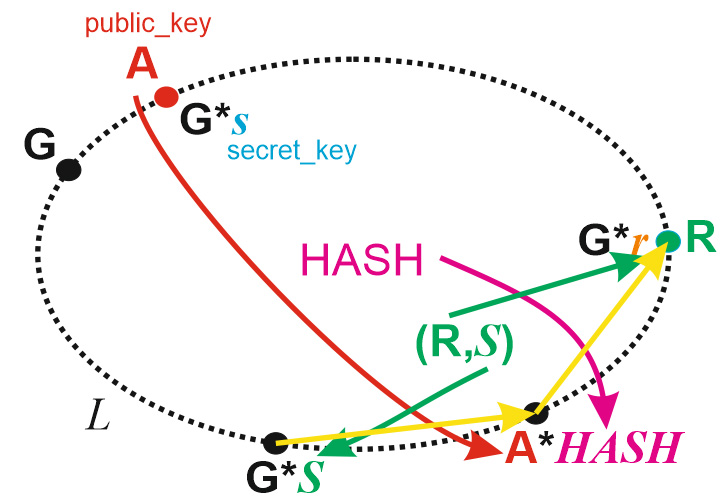
В чем секрет фокуса? Дело в том, что для принятых на E операций сложения и умножения, несмотря на всю сложность их реализации, точно так же выполняется распределительный закон: G * S – A * HASH = G * (r + HASH * s) – G * s * HASH = G * (r + HASH * s – HASH * s) = G * r = R.

Переходим к практике

Надеюсь, такого простого объяснения было достаточно для понимания теории, поскольку далее мы перейдем к суровой практике, а именно к анализу кода. Поскольку реализация алгоритма настолько сложна, что при взгляде на восстановленный псевдокод даже самой простой функции становится жутко, попробуем упростить себе задачу. Для начала найдем готовую реализацию EdDSA и по аналогии разберем логику и структуру алгоритма.

Я считаю самым подходящим кандидатом для сравнения проект Monocypher. Если открыть исходник реализации математических примитивов и восстановленный IDA псевдокод, то создается впечатление, что код компилировался прямо с них. Единственная, но очень досадная помеха — в качестве хеш‑функции в нем используется алгоритм Blake2, тоже довольно экзотический. Возможно, я когда‑нибудь расскажу и о нем, но нам он не подходит, так как у нас используется SHA-512.

На самом деле это не очень большая проблема. Попробуем на примере конкретной сигнатуры проверить работоспособность реализации Monocypher для нашего случая. Вспомним найденную нами ранее функцию верификации сигнатуры sub_140118940 и запишем ее с учетом полученных знаний:

// Верификация сигнатуры, возвращает 0, если успешно, в противном случае 0xFFFFFFFF
// Примерный аналог — crypto_eddsa_check
__int64 __fastcall sub_140118940(__int64 a1)
  // v5=SHA512(R || Public key || License)
  (*(void (__fastcall **)(__int64, char *))(*(_QWORD *)a1 + 24i64))(a1, v5);
    // Обрезает хеш v5 по модулю L, аналог crypto_eddsa_reduce
  sub_1401170F0((__int64)v5);
    // v4 = S, вторая половина сигнатуры
  sub_1401162C0(v4, a1 + 40, 8i64);
    // v3 = –A, где A — публичный ключ a1 + 104 ge_frombytes_neg_vartime
  if ( (unsigned int)sub_140114FA0(v3, a1 + 104) ||
       // Если S > L, то сигнатура неверная is_above_l
     (unsigned int)sub_1401161B0(v4) )
    return 0xFFFFFFFFi64;
    // v3 = G * S – A * HASH
  sub_140114D30(v3, (__int64)v5, a1 + 40);
    // ge_tobytes — преобразование полученного результата из формата расширенных координат в обычный 32-байтовый для последующего сравнения с R
  sub_1401155E0(a1 + 104, v3);
    // Проверка точек на равенство crypto_verify32
  return sub_14000517D(a1 + 8);
}

Как видишь, реализация верификации в нашей программе хоть и аналогичная, но все‑таки немного не такая, как в моносайферовских функциях. Давай все же проверим совместимость этой реализации с нашими хешами. Конечно, по‑хорошему было бы логичным прикрутить к Monocypher хеш‑функцию SHA-512 вместо Blake2, но мы немного схалтурим. Откроем нашу программу в x64dbg и поставим точку останова сразу после вызова sub_1401170F0. Получаем нормализованное по L значение HASH:

3A 8A 86 6E 84 C4 EC 81 5E 0E 77 EB 94 1C 8F 87 35 42 C6 36 64 63 56 12 E3 A0 32 A9 79 95 DE 05

Теперь у нас есть все значения для теста: делаем из них коротенькую тестовую процедурку и вставляем ее в Monocypher.

void test()
{
    u8 public_key[32] = { 0x8F,0xEE,0xEB,0xD8,0x76,0x69,0x7A,0xD5,0x37,0xD4,0x47,0xC7,0x3B,0xBC,0x37,0xC8,0x35,0x63,0x1C,0x93,0xA5,0x0C,0x9F,0x2C,0x55,0x2A,0x01,0x22,0x18,0x7C,0x4E,0x5B };
    u8 h[32] = { 0x3A,0x8A,0x86,0x6E,0x84,0xC4,0xEC,0x81,0x5E,0x0E,0x77,0xEB,0x94,0x1C,0x8F,0x87,0x35,0x42,0xC6,0x36,0x64,0x63,0x56,0x12,0xE3,0xA0,0x32,0xA9,0x79,0x95,0xDE,0x05};
    u8 signature[64] = { 0xF8,0xBF,0xBA,0xE3,0x73,0xE5,0xAC,0x75,0x3F,0x38,0xAC,0xDA,0xF2,0x0C,0x42,0xB1,
        0x80,0x0C,0x18,0xA0,0xBF,0x92,0x8F,0x39,0x5C,0xB1,0xA1,0x8E,0x2E,0xE7,0x47,0x62,0xF1,0x3A,0xE7,0x94,0x2A,0x5F,0x61,0x6D,0x97,0x5F,0x76,0x5B,0xFD,0x82,0xB6,0x58,0xA0,0xD7,0x4C,0x07,0x3B,0x7E,0x61,0xA1,0xB3,0x85,0x75,0x62,0x93,0x94,0x90,0x06 };
    return crypto_eddsa_check_equation(signature, public_key, h);
}

Тест проходит превосходно, и это хорошо — ведь мы, по сути, не имеем ни малейшего представления, как была сгенерирована подпись из нашей программы. Тем не менее подпись прошла верификацию, а значит, Monocypher можно заставить работать и для генерации своей собственной подписи. Давай проверим и эту гипотезу.

Сначала попробуем сгенерировать новые ключи для EdDSA. Для этого выбираем секретный ключ, как произвольное значение crypto_eddsa_key_pair seed — случайно выбранная соль генератора. Чтобы не заморачиваться, сделаем его вообще нулевым:

u8 seed[32] = { 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};
crypto_eddsa_key_pair(secret_key, public_key, seed);

Имеем на выходе:

Публичный ключ

19 d3 d9 19 47 5d ee d4 69 6b 5d 13 01 81 51 d1
af 88 b2 bd 3b cf f0 48 b4 50 31 c1 f3 6d 18 58

Секретный ключ

00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
19 d3 d9 19 47 5d ee d4 69 6b 5d 13 01 81 51 d1
af 88 b2 bd 3b cf f0 48 b4 50 31 c1 f3 6d 18 58

Как видишь, формат хранения секретного ключа у Monocypher вообще халтурный — хранится только соль от него и сгенерированный публичный ключ. Во время всех операций с секретным ключом он тупо восстанавливается из соли, но нам как‑то пофиг: все равно секретный ключ дальше этого тестового кода не пойдет. Теперь попробуем подписать полученным ключом новую лицензию. Для этого воспользуемся кодом процедуры crypto_eddsa_sign:

// secret_key — только что сгенерированный секретный ключ
void crypto_eddsa_sign(u8 signature [64], const u8 secret_key[64],
                        // Совершенно любое сообщение любой длины, по сути, оно требуется нам чисто как соль для r
                       const u8 *message, size_t message_size)
{
    u8 a[64];  // secret scalar and prefix
    u8 r[32];  // secret deterministic "random" nonce
    u8 h[32];  // publically verifiable hash of the message (not wiped)
    u8 R[32];  // first half of the signature (allows overlapping inputs)
    crypto_blake2b(a, 64, secret_key, 32);
    crypto_eddsa_trim_scalar(a, a);
    hash_reduce(r, a + 32, 32, message, message_size, 0, 0);
    crypto_eddsa_scalarbase(R, r);
    // Вот в этом месте тормозим отладчиком исполнение и смотрим полученные значения r и R
    hash_reduce(h, R, 32, secret_key + 32, 32, message, message_size);
    COPY(signature, R, 32);
    crypto_eddsa_mul_add(signature + 32, h, a, r);
    WIPE_BUFFER(a);
    WIPE_BUFFER(r);
}

После вызова crypto_eddsa_scalarbase мы имеем следующее:

R

07 e9 25 9e 9c d4 2d 1a 7c 61 69 54 00 71 b6 47
ff b7 b9 c8 ee d7 06 8b 76 bf 14 5b 6e 22 f0 28

...и соответствующий ему r:

ec cf 58 70 79 3d f9 ab a3 22 19 8e 8c bb 66 72
38 0d 69 1e f2 2e f8 18 a7 39 fd 22 fb 1a 78 06

Теперь нам предстоит снова пересчитать хеш, но уже на основе исправленных R и публичного ключа. Снова запускаем x64dbg, меняем первую половину сигнатуры на R, а старый публичный ключ — на свежесгенерированный. Затем останавливаемся на точке останова вызова sub_1401170F0 и получаем новое значение HASH:

5F DF 27 01 E9 8D C6 40 B7 A0 2F BD 2B 66 FF F5 1E A4 9D 19 58 8B EF F3 8E 8E 1D 99 52 00 F8 07

Заходим обратно в monocypher.c и подставляем значение нового хеша вместо hash_reduce:

void crypto_eddsa_sign(u8 signature [64], const u8 secret_key[64],
                       const u8 *message, size_t message_size)
{
    u8 a[64];  // secret scalar and prefix
    u8 r[32];  // secret deterministic "random" nonce
    u8 h[32] = { 0x5F,0xDF,0x27,0x01,0xE9,0x8D,0xC6,0x40,0xB7,0xA0,0x2F,0xBD,0x2B,0x66,0xFF,0xF5,0x1E,0xA4,0x9D,0x19,0x58,0x8B,0xEF,0xF3,0x8E,0x8E,0x1D,0x99,0x52,0x00,0xF8,0x07 };
    u8 R[32];  // first half of the signature (allows overlapping inputs)
    crypto_blake2b(a, 64, secret_key, 32);
    crypto_eddsa_trim_scalar(a, a);
    hash_reduce(r, a + 32, 32, message, message_size, 0, 0);
    crypto_eddsa_scalarbase(R, r);
//  hash_reduce(h, R, 32, secret_key + 32, 32, message, message_size);
    COPY(signature, R, 32);
    crypto_eddsa_mul_add(signature + 32, h, a, r);
    WIPE_BUFFER(a);
    WIPE_BUFFER(r);
}

На выходе получаем полное значение сигнатуры переподписанной новым ключом лицензии:

07 e9 25 9e 9c d4 2d 1a 7c 61 69 54 00 71 b6 47
ff b7 b9 c8 ee d7 06 8b 76 bf 14 5b 6e 22 f0 28
a5 9c c9 16 19 78 19 cf 69 c5 65 66 9b e3 c8 3c
03 b0 96 8d 07 a1 e8 80 3d fb e7 3e c6 47 be 02

Выводы

Как видишь, мы научились при помощи простого модуля Monocypher, написанного на C, не только подписывать свои данные сигнатурой EdDSA, но и переподписывать чужие. Конечно, я понимаю, что краткость статьи не позволяет охватить множество важных и интересных моментов использования EdDSA: историю создания, различия и преимущества по сравнению с обычным EcDSA, особенности генерации ключей и цифровой подписи, быструю реализацию математических примитивов на эллиптической кривой и многое другое. Если рассказывать обо всем этом, то материала хватит на целую книгу, но цели написать книгу у меня нет. Я надеюсь, что предоставил достаточно ссылок на материалы, с помощью которых любознательный и пытливый читатель сможет найти любую интересующую его информацию об этой технологии.

EdDSA

Исследуем криптоподпись и учимся с ней бороться